Isométrie
I. Définition
A. Activité
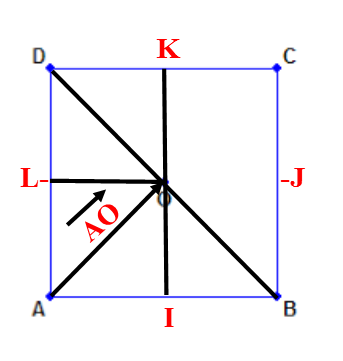
$ABCD$ est un carré de centre $O$. $I$ , $J$ , $K$ , $L$ sont les milieux respectifs des côtés
$[AB] ; [BC] ; [CD] et [DA].$
On note :
- t la translation de vecteur $\overrightarrow{A\! O}$
- S la symétrie orthogonale d’axe $(BD)$
- S’ la symétrie orthogonale d’axe $(IK)$
- SO la symétrie centrale de centre $O$
a) Construire la figure et compléter tableau suivant
b) Comparer la mesure du segment $[AI]$ avec son image par chaque application. Que remarque t-on?
c) Même question pour les triangles $OAI$ et $OAL$
Figure
| A | L | O | [AI] | [AO] | OAI | OAL | |
| Image par t | O | K | C | [OJ] | [OC] | OJC | OKC |
| Image par S | C | K | O | [CI] | [OC] | OJC | OKC |
| Image par S' | B | J | O | [IB] | [OB] | IBO | BJO |
| Image par So | C | J | O | [KC] | [OC] | OKC | OJC |
On remarque que $[AO]=[OC]=[OC]=[OB] =[OC] ; [AI]=[OJ]=[CI]=[IB]=[KC]$ de même les triangles $OAI ;OJC ; OJC ; IBO ; OKC$ ont même dimensions .
On dit que les applications t ; S ; S’ ; SO conservent les distances . Elles sont appelées des isometries ( en grec : ISOS= égale et METRON= mesure).
Le triangle $OCK$ est l’image du triangle $OAI$ par l’isométrie SO ; on dit que les triangles $OCK et OAI$ sont isométriques.
B. Définition
On appelle isométrie toute application du plan qui conserve les distances.
La symétrie centrale, la symétrie orthogonale, la translation.
II. Propriétés des Isométries
A. Activité
Dans l’activité précédente :
1 - A,I ,B sont trois points alignés. Que peut-on dire de leurs images par chacune des
isométries t ; S ; S’ ; SO ?
2 - I est le milieu du segment [AB].Que peut-on dire de l’image de I pour l’image du
segment [AB] par chacune des isométries t ; S ; S’ ; SO ?
3 - Les droites (AB) et (AD) sont perpendiculaires ; que peut –on dire de la position
relative de leur image par chacune des isométries t ; S ; S’ ; SO
4 - Quelle est la mesure de l’angle $\widehat{AOC}$ et de chacune de ses image par les isométries t ; S ; S’; SO
Réponse
1 - Les images de A,I,B sont aussi alignés
2 - L’image de I est aussi milieu de l’image de [AB]
3 - Les images (AB) et (AD) sont aussi perpendiculaires
4 - Les images de l’angle $\widehat{AOC}$ ont la même mesure que l’angle $\widehat{AOC}$
B. Propriété
- Les images par une isométrie de trois points alignés sont trois points alignés.
- L’image par une isométrie du milieu d’un segment est le milieu des images des extrémités de ce segment.
- Les images par une isométrie de deux droites perpendiculaires sont deux droites perpendiculaires.
- Les images par une isométrie de deux droites parallèles sont deux droites parallèles.
- L'image par une isometrie d'un angle est un angle de même mesure.
- L’image par une isométrie d’une surface est une surface de même aire.