Coordonnées d'un Vecteur
I. Coordonnées d’un vecteur du plan
A. Repère du plan
1. Repère du plan
Soient $(D) et (D’)$ deux droites graduées sécantes en leur origine O

(O, $\overrightarrow{i}$, $ \overrightarrow{j}$) définit un repère cartésien du plan.
Remarque :
- On dit que le repère est normé si $OI = OJ =1$
- On dit que le repère est orthonormé si $OI=OJ =1$ et que les axes sont orthogonaux.
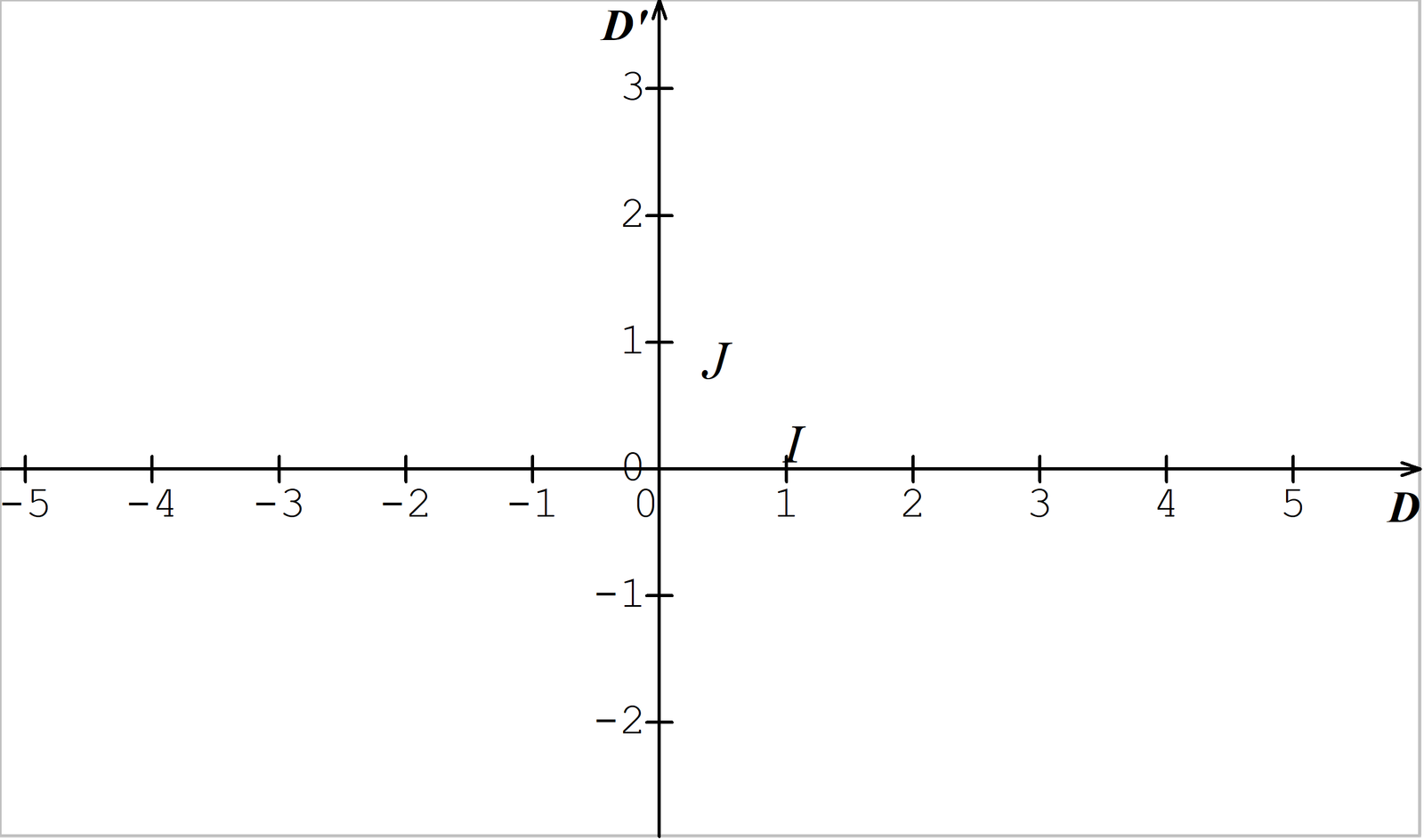
Repère orthonormé : $OI=OJ$ et $(OI)⊥(OJ)$

Repère normé:$OI=OJ$
2. Coordonnées d'un vecteur d'origine O
1 - Activité
Dans un Repère orthonormé , placer le point $A(2 ; 3)$. Donner le vecteur $\overrightarrow{OA}$ en fonction de $\overrightarrow{i}$ et $\overrightarrow{j}$.
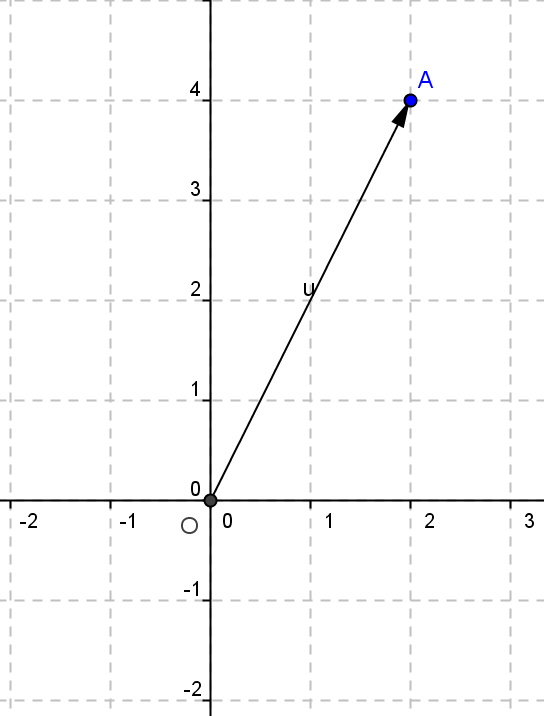
$\overrightarrow{OA}$=2$\overrightarrow{i}$+3$\overrightarrow{j}$ on dit que 2 et 3 sont les coordonnées de $\overrightarrow{OA}$.
Le plan étant muni d’un repère cartésien (O, $\overrightarrow{i}$, $ \overrightarrow{j}$) soit $M$ le point de coordonnées $(x ; y)$. On a alors $\overrightarrow{OM}$=$x\overrightarrow{i}$+$y\overrightarrow{j}$ et on dit que $x$ et $y$ sont les coordonnées de $\overrightarrow{OM}$ dans le repère cartésien (O, $\overrightarrow{i}$, $ \overrightarrow{j}$) on note $\overrightarrow{OM} \left( \begin{array}{clcr} x \\ y \end{array} \right)$.
$\overrightarrow{OM} \left( \begin{array}{clcr} x \\ y \end{array} \right)$ Signifie que $\overrightarrow{OM}$=$x\overrightarrow{i}$+$y\overrightarrow{j}$.
Remarque :
Si $O$ et $M$ sont confondus alors: $\overrightarrow{OM}$=$\overrightarrow{MM}$=$\overrightarrow{OO}$=$\overrightarrow{0}$ de coordonnées $\left(\begin{array}{clcr} 0 \\ 0\end{array} \right)$.
B. Coordonnées d’un vecteur d’ origine O
Activité
Le plan est muni d’un repère cartésien (O ;$ \overrightarrow{j}$ ; $\overrightarrow{j} $) . Soient les points $A$ et $B$ de coordonnées respectives $( x_A ;y_A )$ et $( x_B ; y_B )$ .
1) Exprimer $\overrightarrow{OA}$ et $\overrightarrow{OB}$ en fonction de $\overrightarrow{i}$ et $\overrightarrow{j}$.
2) Exprimer $\overrightarrow{AB}$ en fonction $\overrightarrow{OA}$ et $\overrightarrow{OB}$ a l’aide de la relation de Chasles.
3) Ecrire $\overrightarrow{AB}$ en fonction de $\overrightarrow{i}$ et $\overrightarrow{j}$ et donner les coordonnées de $\overrightarrow{AB}$ dans le repère.
Réponse
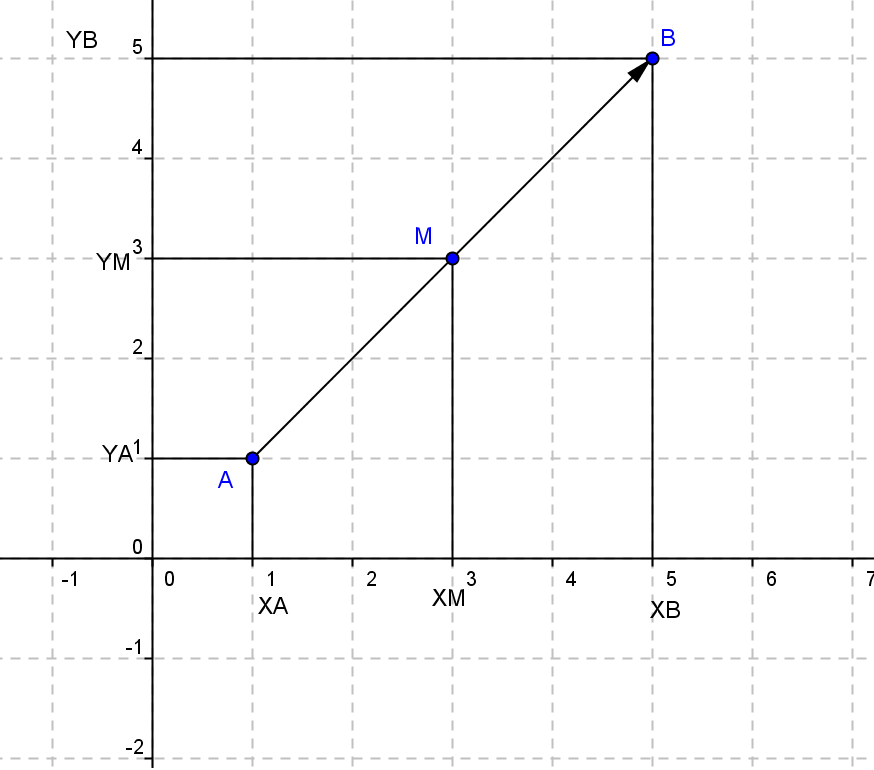
1) $\overrightarrow{OA}$ =$x_A$$\overrightarrow{i}$ Â +$y_A$$\overrightarrow{j}$ et $\overrightarrow{OB}$ =$x_B$$\overrightarrow{i}$ + $y_B$$\overrightarrow{j}$.
2) $\overrightarrow{AB}$ =$\overrightarrow{AO}$+$\overrightarrow{OB}$ = $-\overrightarrow{OA}$ +$\overrightarrow{OB}$=-( $x_A$$\overrightarrow{i}$+ $y_A$$\overrightarrow{j}$ ) + ($x_B$$\overrightarrow{i}$ Â + $y_B$$\overrightarrow{j}$ )= -$x_A$$\overrightarrow{j}$ - $y_A$$\overrightarrow{j}$ + $x_B$$\overrightarrow{i}$ Â + $y_B$$\overrightarrow{j}$ =$x_B$$\overrightarrow{i}$ Â - $x_A$$\overrightarrow{i}$ + $y_B$$\overrightarrow{j}$ Â - $y_A$$\overrightarrow{j}$ $\overrightarrow{AB}$ =$(x_B-x_A)$ $\overrightarrow{i}$ +$(y_B- y_A)$ $\overrightarrow{j}$
$\overrightarrow{AB}\left(\begin{array}{clcr} x_B-x_A\\y_B-x_A \end{array}\right)$.
Propriété
Pour deux point A($x_A$ ; $y_A$) et B($x_B$ ;$y_B$). On a $\overrightarrow{AB}$=($x_B$-$x_A$) $\overrightarrow{i}$ +($y_B$- $y_A$) $\overrightarrow{j}$ on note $\overrightarrow{AB}\left(\begin{array}{clcr} x_B-x_A\\y_B-x_A \end{array}\right)$.
Exercice d’application
Le plan est rapporté a un repère cartésien (O ;$\overrightarrow{i}$ ;$\overrightarrow{j}$) on a A(3 ;1) ; B(-4 ;$\frac{1}{2}$) ; C(0 ;5).
Calculer les coordonnée des vecteurs $\overrightarrow{AB}$ ; $\overrightarrow{AC}$ et $\overrightarrow{BC}$.
C. Coordonnées du vecteur $\overrightarrow{AB}$
Activité
Soient $\overrightarrow{u}\left(\begin{array}{clcr} 4\\5 \end{array}\right)$ $\overrightarrow{v}\left(\begin{array}{clcr} 4\\5 \end{array}\right)$ deux vecteurs du plan. Que peut on dire de ces deux vecteurs ?
On remarque que $\overrightarrow{u}$=$\overrightarrow{v}$.
Soient les vecteurs tels que $\overrightarrow{u}$=$x\overrightarrow{i}$+$y\overrightarrow{j}$ et $\overrightarrow{v}$=$x’\overrightarrow{i}$+$y’\overrightarrow{j}$:
- si $\overrightarrow{u}$=$\overrightarrow{v}$ alors $x=x’$ et $y=y’$;
- si $x=x’$ et $y=y’$ alors $\overrightarrow{u}$=$\overrightarrow{v}$.
Exercice d’ application
On donne A(-3 ; 1) ; B (0 ; 2) ; C(1 ;1) . Déterminer les coordonnées de D tel que $\overrightarrow{AC}$=$\overrightarrow{DC}$.
II. Coordonnées et opérations sur les vecteurs
A. Coordonnées de la somme de deux vecteurs
1- Activité
On donne $\overrightarrow{u}$=2$\overrightarrow{i}$+4$\overrightarrow{j}$ et $\overrightarrow{v}$=-3$\overrightarrow{i}$+5$\overrightarrow{j}$ .Trouver les coordonnées de $\overrightarrow{u}$+$\overrightarrow{v}$
$\overrightarrow{u}$+$\overrightarrow{v}$=(2$\overrightarrow{i}$+4$\overrightarrow{j}$)+(-3$\overrightarrow{i}$+5$\overrightarrow{j}$)
=2$\overrightarrow{i}$+4$\overrightarrow{j}$-3$\overrightarrow{i}$+5$\overrightarrow{j}$
$\overrightarrow{u}$+$\overrightarrow{v}$=$-\overrightarrow{i}$+9$\overrightarrow{j}$)
Les coordonnées de $\overrightarrow{u}$+$\overrightarrow{v} \left( \begin{array}{clcr}-1\\9\end{array} \right)$
Cas général
Soient les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ tels que $\overrightarrow{u}$=$x$$\overrightarrow{i}$+$y$$\overrightarrow{j}$ et $\overrightarrow{v}$=$x'$$\overrightarrow{i}$+$y'$$\overrightarrow{j}$.
$\overrightarrow{u}$+$\overrightarrow{v}$=$x$$\overrightarrow{i}$+$y$$\overrightarrow{j}$+$x'$$\overrightarrow{i}$+$y'$$\overrightarrow{j}$
=$(x+x')$$\overrightarrow{i}$+$(y+y′)$$\overrightarrow{j}$.
2 - Règle
Soient $\overrightarrow{u}\left( \begin{array}{clcr}x\\y\end{array} \right)$ et $\overrightarrow{v}\left( \begin{array}{clcr}x'\\y'\end{array} \right)$. Le vecteur $\overrightarrow{u}$+$\overrightarrow{v} \left( \begin{array}{clcr}x+x'\\y+y'\end{array} \right)$.
B. Coordonnées du produit d’un vecteur par un réel
1 - Activité
On donne $ \overrightarrow{u}$=2 $\overrightarrow{i}$+4$ \overrightarrow{j}$; donner les coordonnées du vecteur 2$ \overrightarrow{u}$; -3$ \overrightarrow{u}$; $\frac{1}{2}\overrightarrow{u}$
2$ \overrightarrow{u}$=2(2 $\overrightarrow{i}$+4$ \overrightarrow{j}$)=4$\overrightarrow{i}$+8$ \overrightarrow{j}$;$ \overrightarrow{u}\left(\begin{array}{clcr} 4 \\ 8\end{array} \right)$
-3$ \overrightarrow{u}$=-3(2 $\overrightarrow{i}$+4$ \overrightarrow{j}$)=-6$\overrightarrow{i}$-12$ \overrightarrow{j}$;-3$ \overrightarrow{u}\left(\begin{array}{clcr} -6 \\ -12\end{array} \right)$
$\frac{1}{2}\overrightarrow{u}$=$\frac{1}{2}$(2 $\overrightarrow{i}$+4$ \overrightarrow{j}$)=$\overrightarrow{i}$+2$\overrightarrow{j}$; $\frac{1}{2}\overrightarrow{u}\left(\begin{array}{clcr} 1 \\ 2\end{array} \right)$.
2 - Cas général
Le plan est rapporté a un repère cartésien (O ;$ \overrightarrow{i}$;$ \overrightarrow{j}$). Soit
$ \overrightarrow{u}$ un vecteur tel que $ \overrightarrow{u}$=$x$$ \overrightarrow{i}$+$y$$ \overrightarrow{j}$ soit k un réel. k$ \overrightarrow{u}$=k($x$$ \overrightarrow{i}$+$y$$ \overrightarrow{j})$= k$x$$ \overrightarrow{i}$+k$y$$ \overrightarrow{j}$.
Alors si on a $ \overrightarrow{u}\left(\begin{array}{clcr} x \\ y\end{array} \right)$ le vecteur k$\overrightarrow{u}$ a pour coordonnées $\left(\begin{array}{clcr} kx \\ ky\end{array} \right)$.
III. Condition de colinéarité de deux vecteurs
A. Propriété
Etant donné $ \overrightarrow{u} \left( \begin{array}{clcr} x \\ y \end{array} \right)$ et $ \overrightarrow{v} \left( \begin{array}{clcr} x' \\ y' \end{array} \right) $
$\rightarrow$ si $ \overrightarrow{u}$ et $ \overrightarrow{v}$ sont colinéaires alors $xy’ +yx’=0$
$\rightarrow$ si $xy’ +yx’=0$ alors$ \overrightarrow{u}$ et $ \overrightarrow{v}$ sont colinéaires.
Remarque
- Soit, dans le plan muni d’un repère orthogonal, les points $A(xA ; yA)$ et $B(xB ; yB)$. Le milieu I du segment [AB] a pour coordonnées $(xI ; yI)$ où : X1=$\frac{Xa+Xb}{2}$ et Y1=$\frac{Ya+Yb}{2}$.
- Soit, dans le plan muni d’un repère orthogonal, les points $A’(xA’ ; yA’)$ symétrique de $A(xA;yA)$ par rapport à $I(xI ; yI)$. Dans ce cas le point $I$ est milieu du segment [AA’].On note $A’=Si(A)$
X1=$\frac{Xa+Xa'}{2}$; $xA’=2xI+xA$
Y1=$\frac{Ya+Ya'}{2}$; $yA’=2yI + yA$ - $M’$ est l’image de $M$ par la translation du vecteur $ \overrightarrow{u}$ se note $M’= t$ \overrightarrow{u}$ (M)$ ↔$\overrightarrow{MM'}$ =$\overrightarrow{u}$ $M(xM ;yM)$ ; $M’(xM’ ;yM’)$ ;$\overrightarrow{u}$ $\left( \begin{array}{clcr} x \\ y \end{array} \right)$ $\overrightarrow{MM'}$ $\left( \begin{array}{clcr} xM'-xM \\ yM'-yM \end{array} \right)$ = $\overrightarrow{u}$ $\left( \begin{array}{clcr} x \\ y \end{array} \right)$
$xM’- xM=x et yM’- yM=y$
$xM’ =x +xM et yM’ =y + yM$
Exercice d’application
Dans le plan muni d’un repère orthonormé ( o,$ \overrightarrow{i}$,$ \overrightarrow{j}$) on donne : $A(-4 ; O)$ $B(2 ; 3)$ ; $C(5 ;-1)$.
1)Soit I milieu de [AB]. Calculer les coordonnées de $I$.
2)Soit $H$ le symétrique de $B$ par rapport à $C$. Calculer les coordonnées de $H$.
3) Soit P l’image de A par la translation de vecteur $ \overrightarrow{BC}$. Calculer les coordonnées de P.