Théorème de Thalès
I. Théorème de Thalès relatif aux triangles
A. Activité
a)Construire un triangle ABC tel que AB=8cm AC=7cm et BC= 6cm.
b)Placer le point E sur (AB) tel que AE=3cm et tracer la parallèle à (BC) passant par E,elle coupe (AC) en F.
c)Mesurer les distances AF ; EF et calculer les rapports $\frac{AE}{AB}$;$\frac{AF}{AC}$;$\frac{AF}{BC}$ et les comparer.
Réponse

3)Calculer $\frac{AE}{AB}$=$\frac{3,42}{7,92}$=0,43 ; $\frac{AF}{AC}$=$\frac{2,16}{4,97}$=0,43; $\frac{EF}{BC}$=$\frac{2,15}{4,98}$=0,43. On dit que les triangles AEF et ABC forment une configuration de Thalès.
B. Définition
On dit que deux triangles forment une configuration de Thalès s’ils sont déterminés par deux droites sécantes coupées par deux droites parallèles.
Exemple
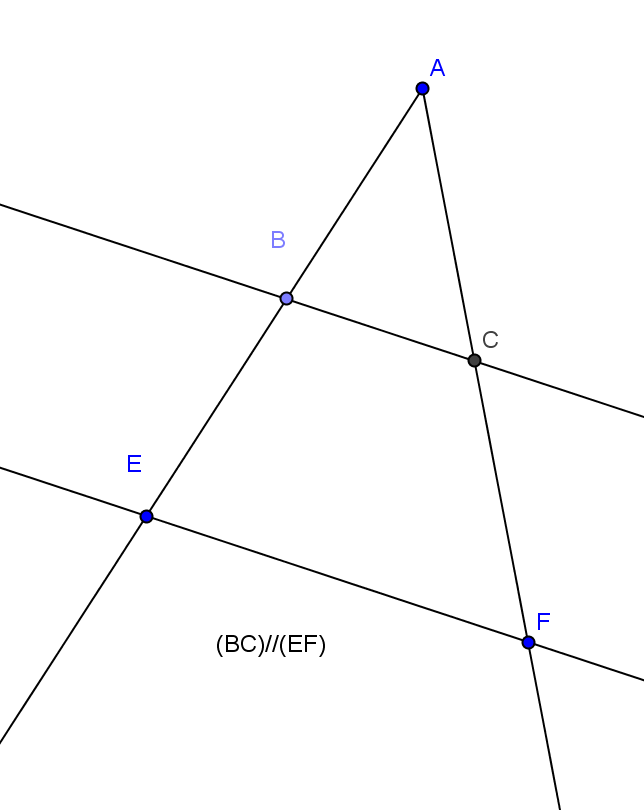
ABC et AEF forment une
Configuration de Thalès
C. Théorème de Thalès
Si les triangles ABC et AEF forment une configuration de Thalès alors $\frac{AE}{AB}$=$\frac{AF}{AC}$=$\frac{EF}{BC}$
Exercice d’application
ABC est un triangle quelconque ; M est un point situé sur le segment [AB] et N est un point situé sur [AC] tel que (MN)//(BC) On a : AB= 7cm ; AC =6cm ; BC = 5cm et AM=2cm.
Calculer les distances AN et MN.
Application du Théorème de Thalès
Partage d’un segment dans un rapport donné.
Soit [AB] un segment , placer un point M sur le segment tel que AM=$\frac{2}{7}$AB.
Reponce
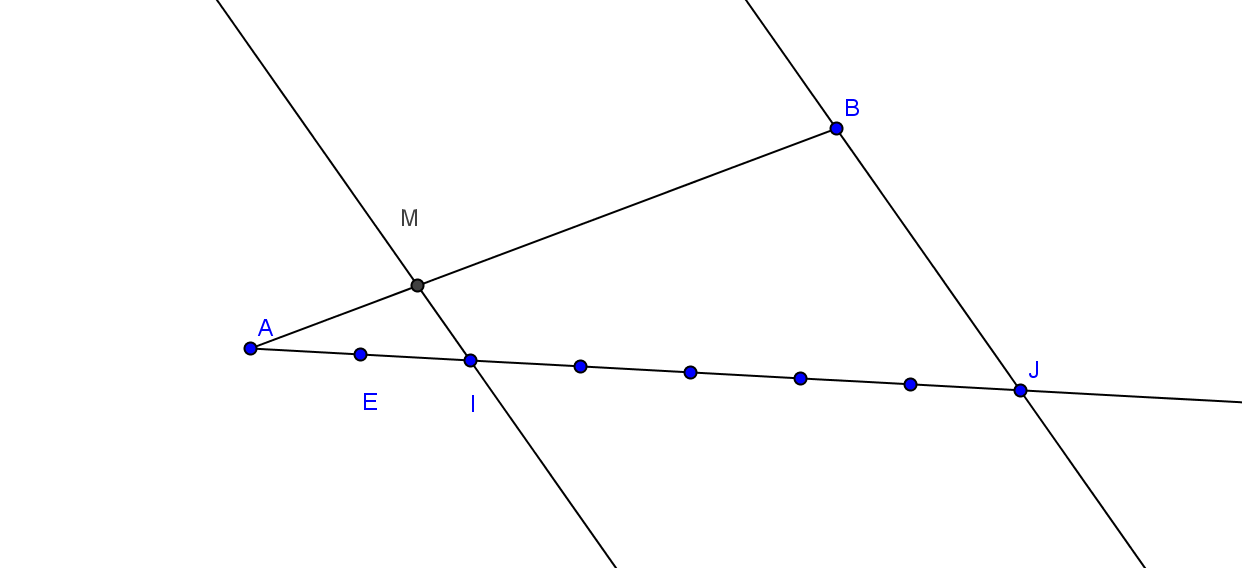
-Traçons le segment [AB]
-Traçons une demi droite [Ax)qui ne passe pas par B -Avec un compas construisons sur [Ax) les points E ; I ;J tel que AE=1 ; AI=2 et AJ=7 -Traçons (BJ) et par I on mène la parallèle à (BJ) elle coupe (AB) en M.
D’après le théorème de Thalès appliqué aux triangles ABJ et AMI, on a :$\frac{AM}{AB}$=$\frac{AI}{AJ}$=$\frac{2}{7}$ alors $\frac{AM}{AB}$=$\frac{2}{7}$ AM=$\frac{2}{7}$AB. On dit qu’on a partagé le segment [AB] dans le rapport $\frac{2}{7}$.
Exercice d’application
Soit un segment [EF] de longueur 8cm. Sans utiliser la règle graduée construire le point M sur la demi droite [EF) tel que EM=$\frac{4}{3}$AG.
Soit ABCD un trapèze. E est le point du segment [BC] tel que BE=$\frac{1}{7}$BC. La parallèle à [DC] passant par E coupe (AD) en F . Démontrer que AF=$\frac{1}{7}$AG
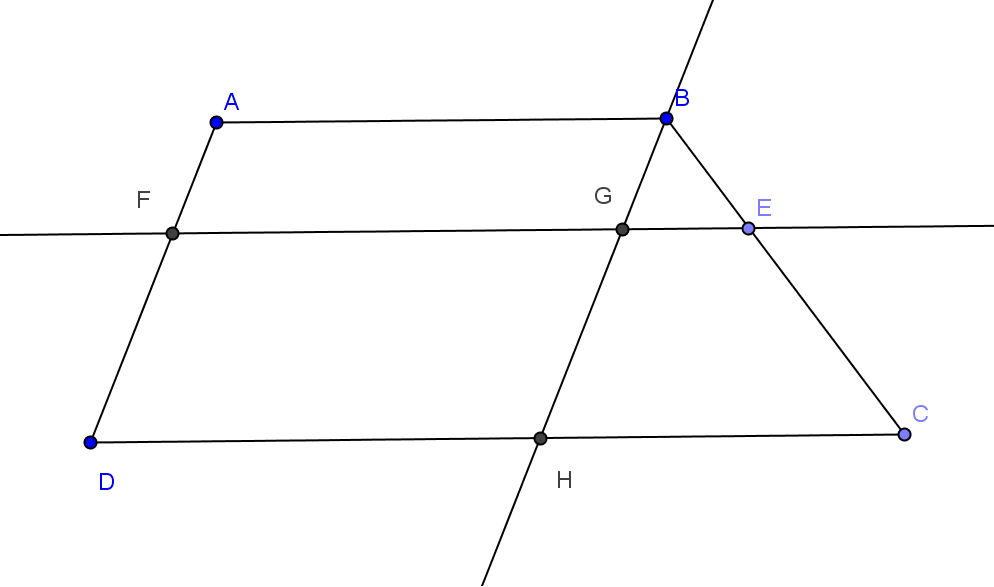
Réponse
Traçons la parallèle à (AD) passant par B elle coupe (EF) en G et (DC) en H. Les triangles BGE et BHC forment une configuration de Thalès alors $\frac{BG}{BH}$=$\frac{BE}{BC}$=$\frac{GE}{HC}$.
ABGF est un parallélogramme donc AF=BG.
ABHD est un parallélogramme donc AD=BH.
$\frac{BG}{BH}$=$\frac{BE}{BC}$ ; $\frac{AF}{AD}$=$\frac{BE}{BC}$ ; $\frac{AF}{AD}$=$\frac{1}{4}$ ; ainsi AF=$\frac{1}{4}$AD.
II. Réciproque du Théorème de Thalès
A. Activité
Soit un segment [AC] de 6 cm .Prendre un point H sur [AC] tel que AH =2cm . Soit B un point n’appartenant pas à (AC). Placer le point D sur le segment [AB] tel que AD =$\frac{1}{3}$AB
a)E est le symétrique de D par rapport à A ; comparer les rapports $\frac{AF}{AB}$ et $\frac{AH}{AC}$ les triangles AEH et ABC forment –ils une configuration de Thalès ?
b)Soit F le symétrique de H par rapport à A. Comparer les rapports $\frac{AE}{AB}$ et $\frac{AF}{AC}$.Les triangles AEF et ABC forment –ils une configuration de Thalès ? Pourquoi ?
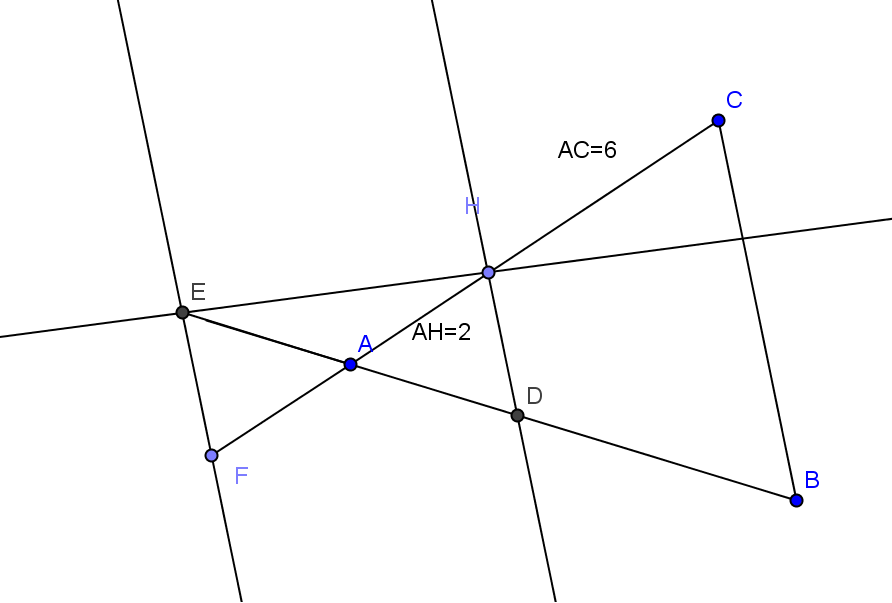
E symétrique de D par rapport à A alors EA =AD
$\frac{AE}{AB}$=$\frac{1}{3}$
$\frac{AH}{AC}$=$\frac{2}{6}$=$\frac{1}{3}$ alors $\frac{AE}{AB}$=$\frac{AH}{AC}$. Les triangles AEH et ABC ne forment pas une configuration de Thalès car (EH) et (BC) ne sont pas parallèles.
AF = AH ; $\frac{AE}{AB}$=$\frac{1}{3}$ ; $\frac{AF}{AC}$=$\frac{2}{6}$=$\frac{1}{3}$ donc $\frac{AE}{AB}$=$\frac{AF}{AC}$. Les triangles AEF et ABC forment une configuration de Thalès car ils sont déterminés par deux droites (EF) et (BC) parallèles coupées par deux droites sécantes.
B. Réciproque du théorème de Thalès
Soit ABC un triangle, E est un point de (AB) si $\frac{AE}{AB}$=$\frac{AF}{AC}$et si $A, B et E$ sont dans le même ordre que $A, C et F$ alors les droites $(BC) et (EF)$ sont parallèles.
Exercice d’application
$(AB) et (IJ)$ sont – elles parallèles ? Justifier
